Make a Regression model to predict house price

Understand Dataset

Data source: the dataset is from Kaggle. I uploaded it into BigQuery as a table called house_table under the dataset called house.

Data Schema:

Type	Type	Mode
price	INTEGER	NULLABLE
area	INTEGER	NULLABLE
bedrooms	INTEGER	NULLABLE
bathrooms	INTEGER	NULLABLE
stories	INTEGER	NULLABLE
mainroad	BOOLEAN	NULLABLE
guestroom	BOOLEAN	NULLABLE
basement	BOOLEAN	NULLABLE
hotwaterheating	BOOLEAN	NULLABLE
airconditioning	BOOLEAN	NULLABLE
parking	INTEGER	NULLABLE
prefarea	BOOLEAN	NULLABLE
furnishingstatus	STRING	NULLABLE

The goal is to predict the housing price based on certain factors like house area, bedrooms, furnished, nearness to main road, etc.

Transform Training Data

In the schema, we observe that the table encompasses various data types including strings, integers, and booleans. To utilize them as features in model training, data transformation is necessary. This transformation can be executed either directly within the create model query or by incorporating a brief preprocessing step to generate a transformed table.

I’ll illustrate the latter method since it’s straightforward to comprehend and convenient for model evaluation and prediction purposes.

• Transform the boolean columns to 1 and 0;
• Transform the string column ‘funishingstatus‘ to 0,1,2
• Store the transformed data into a new table called transformed_table

CREATE OR REPLACE table `house.transformed_table` 
AS
  SELECT 
  price,
  area,bedrooms,bathrooms,stories,parking,
  IF(mainroad, 1, 0) AS mainroad,
  IF(guestroom, 1, 0) AS guestroom,
  IF(basement, 1, 0) AS basement,
  IF(hotwaterheating, 1, 0) AS hotwaterheating,
  IF(airconditioning, 1, 0) AS airconditioning,
  IF(prefarea, 1, 0) AS prefarea,
  CASE 
    WHEN furnishingstatus = 'furnished' THEN 2
    WHEN furnishingstatus = 'semi-furnished' THEN 1
    WHEN furnishingstatus = 'unfurnished' THEN 0
  END AS furnishingstatus

  FROM 
  `instruction-415216.house.house_table`

All columns have been transformed to numerical columns. It will look like this

Row	price	area	bedrooms	bathrooms	stories	parking	mainroad	guestroom	basement	hotwaterheating	airconditioning	prefarea	furnishingstatus
1	2275000	3970	1	1	1	0	0	0	0	0	0	0	0
2	2450000	3240	2	1	1	1	0	1	0	0	0	0	0
3	2450000	7700	2	1	1	0	1	0	0	0	0	0	0
4	2135000	3000	2	1	1	0	0	0	0	0	0	0	0
5	2345000	3640	2	1	1	0	1	0	0	0	0	0	0

Create a Regression Model

Since we completed the preprocessing, the building model step becomes quite simple now.

• model_type='linear_reg' indicates that the model is linear regression.
• input_label_cols=['price'] indicates that the targeted column(label) is price.

CREATE OR REPLACE MODEL `house.regression_model`
OPTIONS
  (model_type='linear_reg',
  input_label_cols=['price']) AS

  SELECT 
    *
  FROM 
  `instruction-415216.house.house_table`

Evaluate Regression Model

SELECT
  *
FROM
  ML.EVALUATE(MODEL `house.regression_model`,
    (
    SELECT
      *
    FROM
      `instruction-415216.house.transformed_table`));
 

The result will look like this

Row	mean_absolute_error	mean_squared_error	mean_squared_log_error	median_absolute_error	r2_score	explained_variance
1	774014.10869855888	1123846260167.2666	0.044876292109699546	568945.76711411029	0.71817696747086464	0.67826837158519

Mean Absolute Error (MAE): This metric calculates the average of the absolute differences between predicted and actual values. It gives a sense of the average magnitude of errors without considering their direction.

Mean Squared Error (MSE): MSE calculates the average of the squared differences between predicted and actual values. It penalizes larger errors more heavily than MAE since errors are squared, making it sensitive to outliers.

Mean Squared Logarithmic Error (MSLE): This metric calculates the mean of the squared differences between the natural logarithm of predicted and actual values. It’s particularly useful when dealing with data that has exponential growth, as it penalizes underestimates more than overestimates.

R-squared (R²): R-squared represents the proportion of the variance in the dependent variable that is predictable from the independent variables. It ranges from 0 to 1, with 1 indicating a perfect fit where the model explains all the variability of the response data around its mean.

Make a Prediction

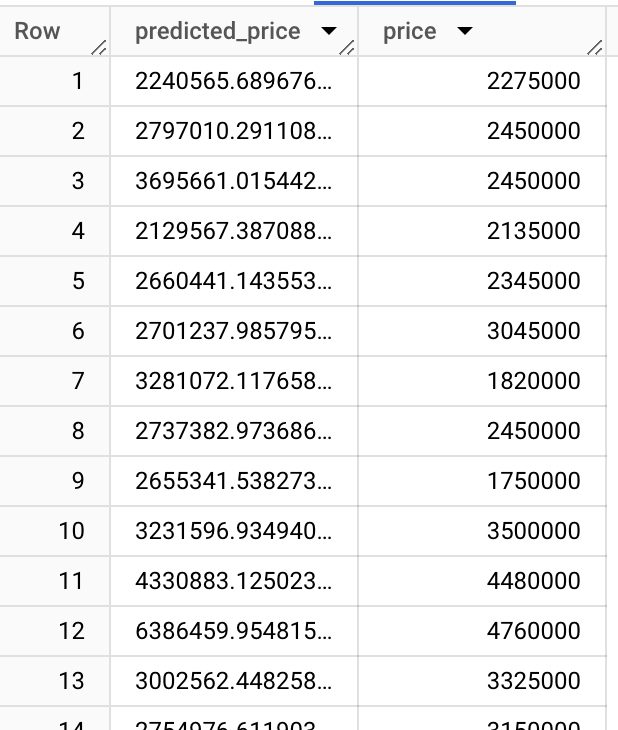
We can visualise it in line graph. It seems that the prediction is not bad.