Overfitting
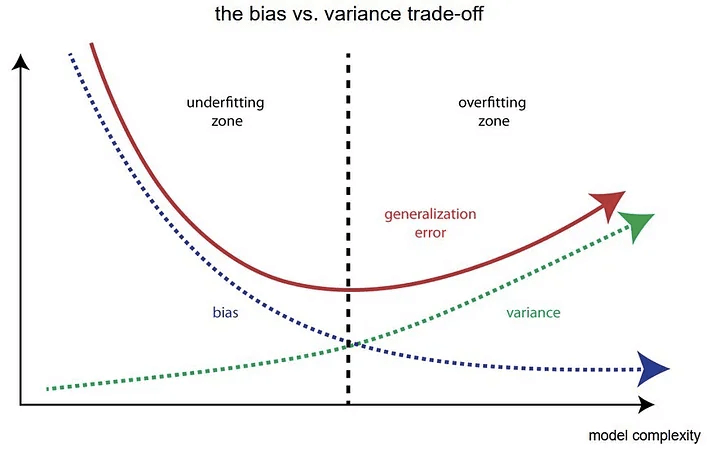
Overfitting is a concept in data science, which occurs when a statistical model fits exactly against its training data. When this happens, the algorithm, unfortunately, cannot perform accurately against unseen data, defeating its purpose.
IBM
The common pattern for overfitting can be seen on learning curve plots, where model performance on the training dataset continues to improve (e.g. loss or error continues to fall or accuracy continues to rise) and performance on the test or validation set improves to a point and then begins to get worse.
In machine learning, L1 regularization and L2 regularization are techniques used to prevent overfitting and improve the generalization of models by adding penalty terms to the loss function during training. Both methods aim to add constraints to the model’s parameters, encouraging simpler and more robust models.
L1 Regularization
L1 Regularization (Lasso Regularization): L1 regularization adds a penalty to the loss function proportional to the absolute value of the model’s parameters. The L1 regularization term is computed as the sum of the absolute values of all the model’s weights multiplied by a regularization parameter (often denoted as λ or alpha).
Mathematically, the L1 regularization term can be expressed as: L1_reg = λ * Σ|w_i|
where w_i represents each individual weight parameter of the model.
The main effect of L1 regularization is that it encourages many of the model’s parameters to be exactly zero, effectively performing feature selection by eliminating less relevant features. This sparsity-inducing property can be useful when dealing with high-dimensional datasets or when you suspect that some features are irrelevant to the task at hand.
L2 Regularization
L2 Regularization (Ridge Regularization): L2 regularization adds a penalty to the loss function proportional to the square of the model’s parameters. The L2 regularization term is computed as the sum of the squares of all the model’s weights multiplied by a regularization parameter (often denoted as λ or alpha).
Mathematically, the L2 regularization term can be expressed as: L2_reg = λ * Σ(w_i^2)
The main effect of L2 regularization is that it discourages large weight values, effectively making the model more robust and less sensitive to small changes in input data. Unlike L1 regularization, L2 regularization doesn’t lead to sparse weight vectors; instead, it tends to distribute the impact of different features more evenly.
Difference between L1 and L2 Regularization
- Penalty Term Formulation: L1 regularization adds the sum of the absolute values of weights, while L2 regularization adds the sum of the squares of weights.
- Sparsity: L1 regularization encourages sparsity by driving some of the weights to exactly zero. L2 regularization does not drive weights to zero but penalizes large weight values, resulting in small but non-zero values for most weights.
- Feature Selection: L1 regularization can perform feature selection by effectively ignoring less important features. L2 regularization does not lead to feature selection in the same way, as it keeps all features with small non-zero weights.
- Computational Efficiency: L2 regularization often has better computational properties during optimization since its derivative is a linear function of weights, while L1 regularization’s derivative is not.
Summary
- If you have a situation where you suspect that many features are irrelevant, choose L1 regularization.
- If you don’t have specific reasons to choose L1 regularization, then choose L2 regularization, as it is generally a good default option and provides a more continuous and stable regularization effect.
- You can combine L1 and L2 regularization together, which is called Elastic Net regularization. It can get the benefits of both techniques.